Work!

Today, we further explored work, going into more depth than just Work = Force x Displacement!

From the in class work and more discussion with group members, we were able to learn a lot about work. Here’s a short recap:

1) Doing work in physics is specifically about moving objects with a force. Unlike everyday life, where we interpret “doing work” as “expending energy”, in physics it is possible to use energy that does not achieve any work. For example, when a student pushes on a wall but doesn’t move it, they would have expended energy, but since the wall didn’t move no work would have been done.

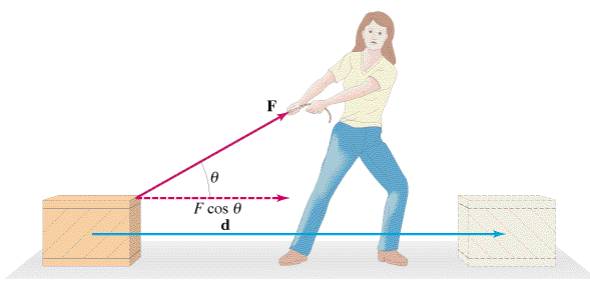
2) Work can be positive or negative. Positive work is done when the force applied and the displacement are in the same direction. Negative work is done when the force applied and the displacement are in opposite directions. This means that our original equation, W = FΔd should now be updated to W = |FΔd|cosΘ, where Θ is the angle difference between the direction of the force and the direction of the displacement. Note that since cos 90° is equal to zero, when the the displacement is perpendicular to the applied force, the work done is zero.

3) Each force on an object has its own value of work done. We can sum up all the work being done on the system to get the net work on the system, W_net = ΣW. Another way to find the net work is by using the net force on the system and the displacement, W_net = |F_netΔd|cosΘ. If the net work is positive, the system gains kinetic energy. Likewise, if the net work is negative, the system loses kinetic energy. This is called the kinetic energy - net work theorem and is represented by the expression: W_net = E_{k final} - E_{k initial} = ΔE_k.

That’s quite a lot to take in, and I still have a few questions.

1) Since work depends on the direction of the force and the direction of the displacement, why isn’t it a vector?

2) With W = FΔd, a gain in gravitational potential energy would result in an increase in work. Would the equation W_net = E_{k final} - E_{k initial} = ΔE_k have also applied to a change in gravitational potential energy? If so, that would mean that work is a change in mechanical energy. The equation would look like this: W_net = (E_{k final} - E_{k initial}) + (E_{g final} - E_{g initial}) = ΔE_mech.

Something interesting that I found out today is that when drawing LOL diagrams to show the transfer of energy, we can simply extend the LOL diagram further to show multiple stages of energy transfer! We then get an LOLOLOLOL… diagram!

After Unit Reflection

Understanding Energy - Work

In this blog post, I gained an understanding of the concept of work in physics! I made an important distinction between the physics definition of work compared to everyday life: work in physics is about moving objects with a force, or changing the energy of a system, while work in everyday life is about putting in the effort. I learned how to calculate work with the equation Wnet =

FnetΔd

cosΘ and noted that it was a scalar and had a special unit: the joule (symbol: J). In addition, I found that each force has their own value of work done, and that the net work represents the total change in energy, which can be used to determine if the system is gaining or losing energy.